seuOJ218 - 简单的色子

• 题目类型：传统
• 输入文件：标准输入流
• 输出文件：标准输出流
• 时间限制：1000 ms
• 空间限制：256 MiB
• 题目标签：夏季, 校赛, 2019

题目描述

众所周知，色子共有六面，我们对色子的六个面分别编号为 $1,2,3,4,5,6$，我们用一个平面图来描述一个色子，两个色子对于的平面图还能用一个矩阵来描述，具体转换方式如下图：

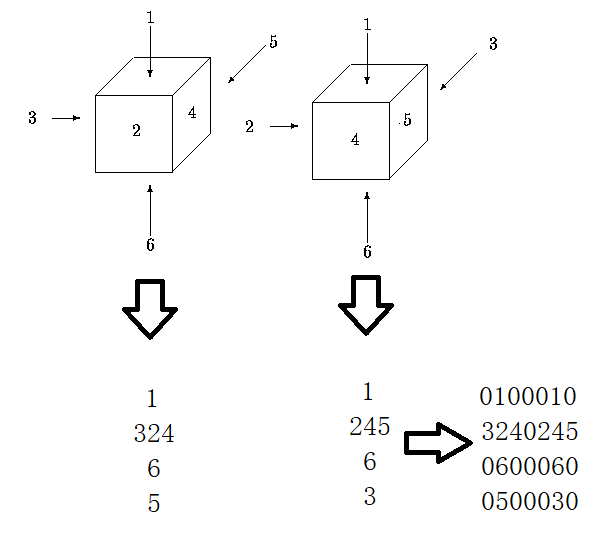
我们发现，有一些不同的色子可以通过如下 $6$ 种旋转（旋转均为 $90°$），使得对应的平面图完全相同：

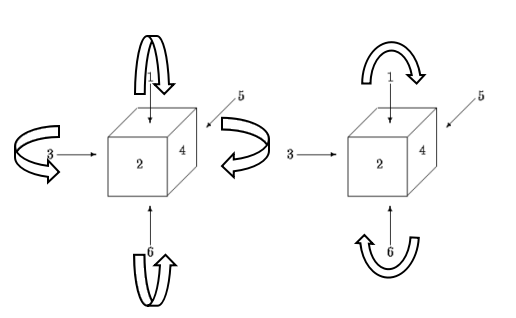
现在我们有很多对色子，我们想知道，每对色子能否通过旋转其中某一个色子，使得两个色子对应的平面图完全相同。

输入格式

输入数据的第一行共一个整数 $T(1\leq T\leq 10^3)$ 表示测试数据组数，接下来为每组测试数据内容。

对于每组测试数据，共 $4$ 行，每行 $7$ 个字符，表示两个色子对应的平面图的矩阵描述结果。

输出格式

对于每组测试数据，输出一行共一个字符串。

• 如果是可以通过旋转其中某一个色子，使得两个色子对应的平面图完全相同，输出一个字符串 "YES x"（请将其中的 x 替换为最小旋转次数）。
• 否则输出一个字符串 "NO"。

样例

样例输入

2
0500020
3140364
0200050
0600010
0400030
1260126
0300040
0500050

样例输出

YES 2
NO