seuOJ106 - 概率作业

• 题目类型：传统
• 输入文件：标准输入流
• 输出文件：标准输出流
• 时间限制：2000 ms
• 空间限制：256 MiB
• 题目标签：秋季, 校赛, 2018

题目描述

lcl 最近很忙，但是他又必须完成他的老师给他布置的作业，于是 lcl 想到了他的朋友 cqh，然后他把题目丢给 cqh，但是 cqh 不屑于做这种简单题，所以 lcl 只好找到了你。

这道题目是这样的：有一个 $n\times n$ 的正方形网格，从 $(0,\ 0)$ 到 $(n-1,\ n-1)$ 标号，网格中有 $k$ 个无法通过的大小为 $1\times 1$ 的障碍物被放置在一些网格内。RandomWalker 一开始落在网格的左上角 $(0,\ 0)$，每一秒它会以相等的可能性留在原地或者移动到相邻的没有障碍物的方格内(我们称两个方格是相邻的，当且仅当它们拥有一条公共边)，如下图所示 RandomWalker 为在网格边界上时的行动规则。

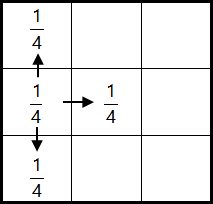
上述过程经过了无数年后，没人知道 RandomWalker 所在的具体位置。为了减小搜索面积，Questioner 希望你计算出 RandomWalker 现在所处位置$(x,\ y)$ 在方格右下三角内的概率(即 $x+y\geq n-1$ 的概率)。

输入格式

输入数据第一行包含一个数 $T(1\leq T \leq 10^3)$，表示数据组数。

对于每组数据，第一行包含两个数 $n(1\leq n\leq 10^4)$ 和 $k(1\leq k\leq 10^3)$，意义如题目中所描述。

接下来 $k$ 行，每行包含两个数，表示每个障碍物的坐标。

数据保证，起始点 $(0,\ 0)$ 没有障碍物，并且图中去除障碍物后的部分是连通的。

输出格式

对于每一组测试数据，输出一行，内容为答案。

为避免精度问题，答案将输出为分数形式，形如p/q，你的答案需保证 $gcd(p,\ q)=1$。

样例

样例输入

5
3 0
3 1
1 1
3 2
1 1
2 2
3 3
1 1
1 2
2 2
5 4
1 1
1 2
2 3
3 2

样例输出

2/3
5/8
10/19
7/16
43/71