hy_peng big genshin! - 帖子

序言

你以为的短码编程讲座
1. 优雅的删掉空格
2. 使用 cin 而不是 scanf
3. bits/stdc++.h
实际上的短码编程讲座
1. 循环融合
2. 可控内存溢出
3. 寄存器分析
4. main 递归

基本规则

一共五题，每题 $100$ 分，选手的分数如下计算：

如果选手未能 AC 此题，此题记 $0$ 分。
如果选手成功 AC 此题，分数为： $\Large s_u=100^{\sqrt{\frac{l_min}{l_{u}}}}$ ，其中 $s_u$ 表示选手分数， $l_u$ 表示选手代码长度， $l_{min}$ 表示所有 AC 此题的选手中最短代码长度。
选手代码原始代码长度 $l'_u$ 计算方式：考虑空格和换行，计算所用的字节数，以 SEUOJ 提交记录显示的数字为准。
选手代码长度 $l_u$ 计算方式： $l_u=l'_u\times c_p$ ，其中 $c_p$ 表示语言系数，Python 为 $2.0$ ，其它语言 $1.0$ 。

短码编程

GNU's Not Unix

这个规则下其它语言没得打，想拿奖老老实实用 C（不是 C++）语言。

比赛的编译器是 GNU 系列的 GCC，下面技巧均针对 GCC。其它编译器（MSVC 等）大概率通不过编译，尤其注意 Visual Studio 默认编译器是 MSVC，用不了。

恶补编译基本知识

VS-VSC
GCC-MSVC（GNU89）
O2 or NOT
DEVC++

从刷榜开始

不妨从去年的第一题开始刷榜，尝试写出比冠军短得多的代码。

最终代码

删去空格和换行的提交版本：

#define l a[i*m+j]
#define F for(i=1;n/i;i++)for(j=1;m/j;j++)
float a[~0u],s[9];main(f,n,m,i,j){scanf("%d%d",&n,&m);F scanf("%f",&l),!a[j]||a[j]>l&&l?a[j]=l:0;F l&&(s[i]+=pow(99,sqrt(a[j]/l)))>s[f]?f=i:0;printf("%d",f);}

格式化后版本：

#define l a[i * m + j]
#define F                   \
    for (i = 1; n / i; i++) \
        for (j = 1; m / j; j++)
float a[1 << 24], s[9];
main(f, n, m, i, j) {
    scanf("%d%d", &n, &m);
    F scanf("%f", &l), !a[j] || a[j] > l && l ? a[j] = l : 0;
    F l && (s[i] += pow(99, sqrt(a[j] / l))) > s[f] ? f = i : 0;
    printf("%d", f);
}

去年冠军此题代码长度为 281Byte，我这份代码长度为 222Byte，按照计分规则，他只能拿到 $59.93$ 分，甚至没能及格。

基本技巧

大部分函数不写 #include 也能用。
main 函数可以不写 return 0;。
全局变量不写定义默认是 int。
全局变量初值全为 0。
函数，写参数时可以省略类型，返回值类型也可以省略，默认是 int。
main 函数参数，可以有任意多个，第一个参数默认为 1，其余都是随机数。

用基本技巧写个 A+B

main(a,b){scanf("%d%d",&a,&b);printf("%d",a+b);}

为什么非要在 main 参数里面定义变量？

先写个能对的

double s[1005];
a[1005][1005], mv[1005];
main(f, n, m, i, j) {
    memset(mv, 1, sizeof(mv));
    scanf("%d%d", &n, &m);
    for (i = 0; i < n; i++)
        for (j = 0; j < m; j++){
        	scanf("%d", &a[i][j]);
            if(mv[j] > a[i][j] && a[i][j])
                mv[j] = a[i][j];  
        } 
    for (i = 0; i < n; i++)
        for (j = 0; j < m; j++)
            if(a[i][j])
                s[i] += pow(100, sqrt(1. * mv[j] / a[i][j]));
    for (i = 0; i < n; i++)
        if (s[i] > s[f])
            f = i;
    printf("%d", f + 1);
}

公共子表达式

观察到 a[i][j] 出现的次数比较多，所以写个宏替换一下：566->549（我们还没删空格和换行，所以字节数看起来比较大。）

#define l a[i][j]
double s[1005];
a[1005][1005], mv[1005];
main(f, n, m, i, j) {
    memset(mv, 1, sizeof(mv));
    scanf("%d%d", &n, &m);
    for (i = 0; i < n; i++)
        for (j = 0; j < m; j++){
        	scanf("%d", &l);
            if(mv[j] > l && l)
                mv[j] = l;  
        } 
    for (i = 0; i < n; i++)
        for (j = 0; j < m; j++)
            if(l)
                s[i] += pow(100, sqrt(1. * mv[j] / l));
    for (i = 0; i < n; i++)
        if (s[i] > s[f])
            f = i;
    printf("%d", f + 1);
}

循环出现的次数似乎也有点多了，可以替换掉：549->475（其实有一部分是少掉的空格导致的，但是实际上也确实少了不少字符）

#define l a[i][j]
#define F for (i = 0; i < n; i++) for (j = 0; j < m; j++)
double s[1005];
a[1005][1005], mv[1005];
main(f, n, m, i, j) {
    memset(mv, 1, sizeof(mv));
    scanf("%d%d", &n, &m);
    F{
        scanf("%d", &l);
        if(mv[j] > l && l)
            mv[j] = l;
    } 
    F
        if(l)
            s[i] += pow(100, sqrt(1. * mv[j] / l));
    for (i = 0; i < n; i++)
        if (s[i] > s[f])
            f = i;
    printf("%d", f + 1);
}

另外注意到，最后一个循环，再循环一层 $j$ 一点问题都没有，只是把这部分代码多执行了 $m-1$ 遍，反正是取最大值，干脆一并换掉：475->453。

#define l a[i][j]
#define F for (i = 0; i < n; i++) for (j = 0; j < m; j++)
double s[1005];
a[1005][1005], mv[1005];
main(f, n, m, i, j) {
    memset(mv, 1, sizeof(mv));
    scanf("%d%d", &n, &m);
    F{
        scanf("%d", &l);
        if(mv[j] > l && l)
            mv[j] = l;
    } 
    F
        if(l)
            s[i] += pow(100, sqrt(1. * mv[j] / l));
    F
        if (s[i] > s[f])
            f = i;
    printf("%d", f + 1);
}

真的要初始化吗？

memset(mv, 1, sizeof(mv)); 占了 26 字符，能删掉吗，答案是可以，只需要在更新 mv[j] 时加上 mv[j]==0 的条件即可：453->431。

#define l a[i][j]
#define F for (i = 0; i < n; i++) for (j = 0; j < m; j++)
double s[1005];
a[1005][1005], mv[1005];
main(f, n, m, i, j) {
    scanf("%d%d", &n, &m);
    F{
        scanf("%d", &l);
        if(!mv[j] || mv[j] > l && l)
            mv[j] = l;
    } 
    F
        if(l)
            s[i] += pow(100, sqrt(1. * mv[j] / l));
    F
        if (s[i] > s[f])
            f = i;
    printf("%d", f + 1);
}

逻辑运算符的顺序。
用 ! 来替代 ==0。
有时候可以用指针来滚动数组代替初始化。

此时，删去空格和换行，发现代码已经来到了 256，已经超过去年冠军了。

#define l a[i][j]
#define F for(i=0;i<n;i++)for(j=0;j<m;j++)
double s[1005];a[1005][1005],V[1005];main(f,n,m,i,j){scanf("%d%d",&n,&m);F{scanf("%d",&l);if(!V[j]||V[j]>l&&l)V[j]=l;}F if(l)s[i]+=pow(100,sqrt(1.*V[j]/l));F if(s[i]>s[f])f=i;printf("%d",f+1);}

分支？那是什么？

if() 占了足足四个字符，而且还无法被解析为一条语句，浪费了两个字符 {} 来限定域，因此可以利用三目运算符来省略掉分支：

#define l a[i][j]
#define F for(i=0;i<n;i++)for(j=0;j<m;j++)
double s[1005];a[1005][1005],V[1005];main(f,n,m,i,j){scanf("%d%d",&n,&m);F scanf("%d",&l),!V[j]||V[j]>l&&l?V[j]=l:0;F l?s[i]+=pow(100,sqrt(1.*V[j]/l)):0;F s[i]>s[f]?f=i:0;printf("%d",f+1);}

比较 if() 和 ?:0，少了一个字符，现在变成 253 了。

问苍天，借内存 4K

C 的内存分配采用堆-栈-核心-代码-数据五层，利用堆栈之间的预留内存以及二维数组内存运算机制可以进行合理溢出操作。

特别注意，溢出操作的可行性和内存分配机制有较大关系，可能需要微调前面的大数组的大小数据类型，溢出的内存初值不可控，对初值有严格要求的代码不适用溢出操作。

这里 V 对初值要求严格，s 相对弱一点，s 只要保证初值全一样就能 work。

#define l a[i][j]
#define F for(i=0;i<n;i++)for(j=0;j<m;j++)
a[2048][999];float V[2048],s[9];main(f,n,m,i,j){scanf("%d%d",&n,&m);F scanf("%d",&l),!V[j]||V[j]>l&&l?V[j]=l:0;F l?s[i]+=pow(100,sqrt(1.*V[j]/l)):0;F s[i]>s[f]?f=i:0;printf("%d",f+1);}

代码长度来到 247。

自动寻址的你已经 out 了

数组的定义很长，特别是那个二维的，能不能定义成一维？

当然可以我的朋友！

#define l a[i*m+j]
#define F for(i=0;i<n;i++)for(j=0;j<m;j++)
a[1<<22];float V[2048],s[9];main(f,n,m,i,j){scanf("%d%d",&n,&m);F scanf("%d",&l),!V[j]||V[j]>l&&l?V[j]=l:0;F l?s[i]+=pow(100,sqrt(1.*V[j]/l)):0;F s[i]>s[f]?f=i:0;printf("%d",f+1);}

代码长度继续减小到 244，此时我们发现，V 的数据类型并不重要，而 a 其实被空了一截出来，V 可以用上这部分空的值，当然，我们得稍微移动一下 a 的下标，让数据从 1 开始编号，这样 f+1 也能被省略为 f 了。

#define l a[i*m+j]
#define F for(i=1;i<=n;i++)for(j=0;j<m;j++)
a[1<<22];float s[9];main(f,n,m,i,j){scanf("%d%d",&n,&m);F scanf("%d",&l),!a[j]||a[j]>l&&l?a[j]=l:0;F l?s[i]+=pow(100,sqrt(1.*a[j]/l)):0;F s[i]>s[f]?f=i:0;printf("%d",f);}

不妨牺牲一下精度，例如将 100 换成 99，显然，我们运气很好，没有任何问题。

#define l a[i*m+j]
#define F for(i=1;i<=n;i++)for(j=0;j<m;j++)
a[1<<22];float s[9];main(f,n,m,i,j){scanf("%d%d",&n,&m);F scanf("%d",&l),!a[j]||a[j]>l&&l?a[j]=l:0;F l?s[i]+=pow(99,sqrt(1.*a[j]/l)):0;F s[i]>s[f]?f=i:0;printf("%d",f);}

思路打开了，现在来到 234。

跨越时空的相遇——循环融合

第三个循环真的是必须的吗？

是否可以在计算 s[i] 的同时就计算 f 呢，显然可以，因为 s[i] 加上最后一个有效值时，就一定会完成一次有效比较。

将第三个循环的统计放入第二个循环：

#define l a[i*m+j]
#define F for(i=1;i<=n;i++)for(j=0;j<m;j++)
a[1<<22];float s[9];main(f,n,m,i,j){scanf("%d%d",&n,&m);F scanf("%d",&l),!a[j]||a[j]>l&&l?a[j]=l:0;F l?s[i]+=pow(99,sqrt(1.*a[j]/l)):0,s[i]>s[f]?f=i:0;printf("%d",f);}

代码长度来到 232。

左，左，还能左——利用运算符的返回值

s[i]+=s[j]+=3;

+= 操作的返回值是对左操作数的左值，利用这个特性，第二个 s[i] 可以被省略掉：

#define l a[i*m+j]
#define F for(i=1;i<=n;i++)for(j=0;j<m;j++)
a[1<<22];float s[9];main(f,n,m,i,j){scanf("%d%d",&n,&m);F scanf("%d",&l),!a[j]||a[j]>l&&l?a[j]=l:0;F l?(s[i]+=pow(99,sqrt(1.*a[j]/l)))>s[f]?f=i:0:0;printf("%d",f);}

来到 229，由于运算顺序，必须要给 s[i]+= 带上括号。

短路吧！我的逻辑运算！

我们用 ?: 操作符需要一个额外的 0 来补位，但是 C 的二元逻辑操作符，例如 && 和 ||，在计算完第一个值后如果能确定结果，就不会计算第二个值，这样就可以用两个符号来实现 if，代码长度变为 228，再将 a 改为 float 以便删掉之前由于需要使用整数除法额外添加的 1.*，代码长度可以控制到 225。

最后，i<=n 在 $i\ne 0$ 时可以用 n/i 替代，所以来到 224。

#define l a[i*m+j]
#define F for(i=1;n/i;i++)for(j=0;j<m;j++)
float a[1<<22],s[9];main(f,n,m,i,j){scanf("%d%d",&n,&m);F scanf("%f",&l),!a[j]||a[j]>l&&l?a[j]=l:0;F l&&(s[i]+=pow(99,sqrt(a[j]/l)))>s[f]?f=i:0;printf("%d",f);}

总结

224 就是我使用常规方法能够达到的最短长度了，222 的那份提交使用了一些非常规方法，不在本堂讲座内容范畴。

当然我不是专业的短码选手，222 肯定也不是理论最短代码长度，欢迎挑战更短。

语法技巧

自动查找定义

C++ 部分头文件里面写 #include<xxx.h> 之后会自动包含在全局命名空间，不需要 std::。
C++ 支持 Objective-C 的写法，可以 #import<xxx>。

利用库函数的返回值

cin 在读到 EOF 时返回 0。
scanf 读到 EOF 时返回 -1，否则返回 0，利用 EOF 的特性，可以在某些时候不读入数据个数。
puts 的返回值一般是 0，可以配合全局变量用于在循环内初始化一些值。

稀奇古怪的运算符返回值

+= 系列：返回左操作数的左值。
,：逗号运算符的返回值是右边语句的返回值。

库函数

atoi：字符串转 int，由于用 gets() 读入字符串比用 scanf() 和格式化符号读入整数要短得多，所以有时候是有意义的。
bsearch：和 cpp 的 lower_bound 差不多，自行查手册。
qsort：和 cpp 的 sort 差不多，自行查手册。
itoa：将整数转为 base 进制字符串。
strtol：上面的反函数，结合 puts 使用有奇效。
hypot：给定两点横纵坐标差，计算距离。
strstr：从字符串中查找指定的子串，返回查找到的位置。

利用位运算

表示一个大整数时，最好用 1<<20 等方法表达，如果不用于定义数组，1e9 会更好。
表示一个特定的大数时，可以使用字符常量，例如用 'ab' 表示 24930，这是把 a 的十六进制和 b 的十六进制拼接的结果，24930=256*97+98

用 for 循环而不是 while

for(;;) 和 while() 的长度是一样的，for(;;) 里面可以加一些语句，可以省掉 ;。

类型隐式强转

printf 的逻辑是以某种格式读取数据并输出，%d 并不会将 float 强转为 int 后输出，而是直接读取 float 变量内存中的值并将其解析为 int 再输出。

关于运算符顺序的一些碎碎念

&& 这些用于短路分支的时候，= 的优先级比较低，所以 a&&b=c 会编译错误，因为顺序是 (a&&b)=c，而 a&&b++ 就没有问题，++ 运算的优先级比 && 高。

实践

输入十二个数，输出它们的平均值

b;main(a){for(;~scanf("%d",&a);b+=a);printf("%.2f",b/12.);}

print(f"{sum(int(input())for _ in[0]*12)/12:.2f}")

题面如下：

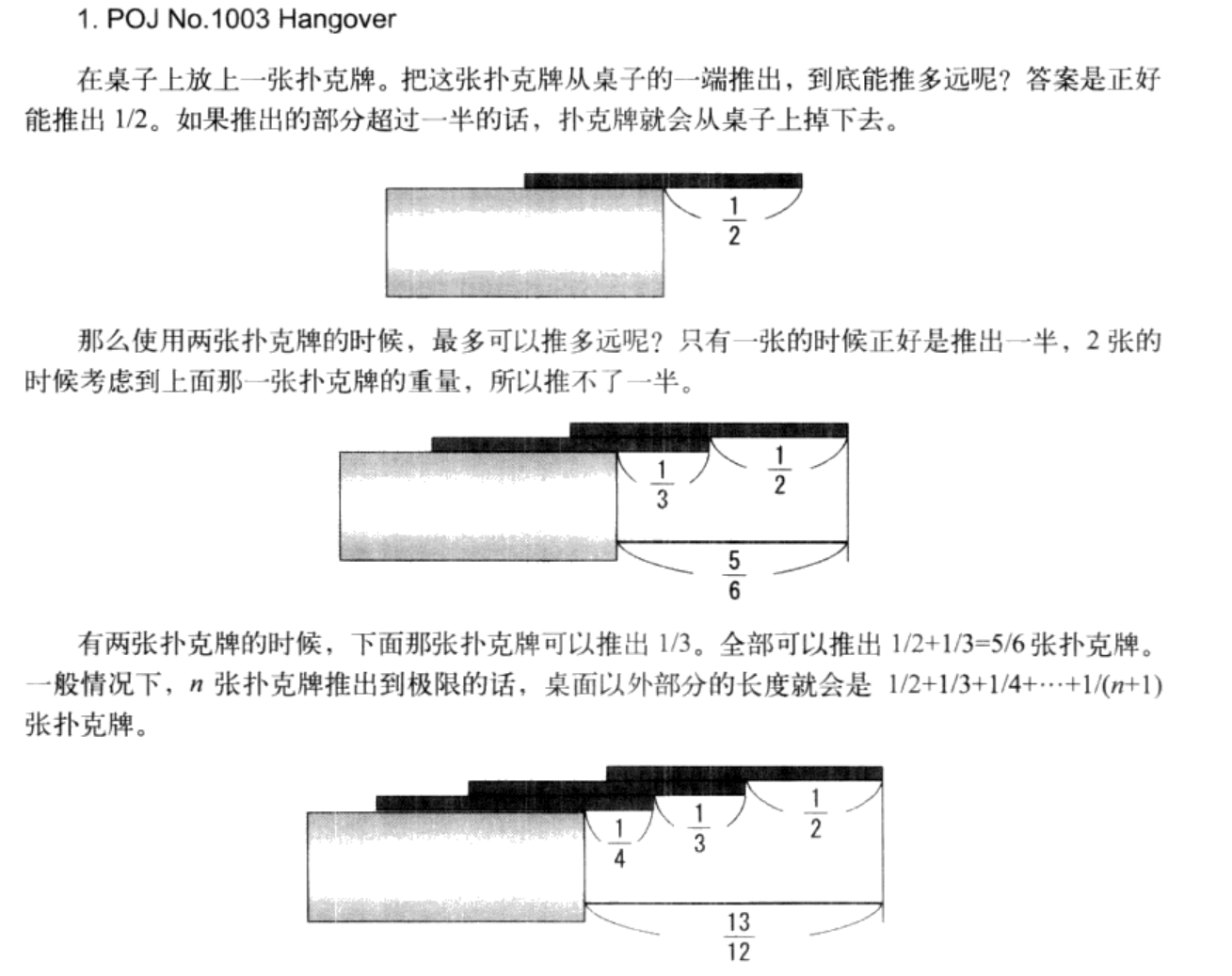
多组数据，问给定一个长度 $f$ ，至少需要多少张牌才能推出达到长度 $f$ 。
```
main(n){float b;for(;n=scanf("%f",&b),~n;printf("%d card(s)\n",n-1))for(;b>0;)b-=1./++n;}
```
输入一个数 $n$ ，接下来 $n$ 个数 $a_i$ ，对于每个 $a_i$ ，输出 $\lfloor\sqrt a_i\rfloor$ 。

对原问题做若干数学推导之后变成了这个简化问题，代码如下：
```
i;main(k){for(;~scanf("%d",&k);)i++&&printf("%d\n",k=sqrt(k));}
main(i,k){for(;gets(&k);)--i&&printf("%d\n",i=sqrt(atoi(&k)));}
main(i,k){for(;gets();)--i&&printf("%d\n",i=sqrt(atoi()));}
```
前两行基本没啥问题，第三行非常逆天，但是第三行的程序只能在 32bit 的机子上运行，原理是利用负责传参的帧栈指针指向的随机地址空间。

很遗憾，SEUOJ 不提供 32bit 编译环境，所以第三行的语法用不了。

省略函数返回值

有时候你不得不写函数，return 有点长，#define 实现函数也不太行，但是，其实函数不一定要写返回值。

代码

c;f(a,b){c=a+b;}main(a){scanf("%d%d",&a,&b);printf("%d",f(a,b));}

汇编代码分析

f(a,b){
    return a+b;
}

以上代码的汇编是：

push    rbp
mov     rbp, rsp
mov     DWORD PTR [rbp-4], edi
mov     DWORD PTR [rbp-8], esi
mov     edx, DWORD PTR [rbp-4]
mov     eax, DWORD PTR [rbp-8]
add     eax, edx
pop     rbp
ret

C 语言约定函数返回值通过 eax 寄存器传递，所以只要想办法用上 eax 寄存器让它保存最后的值就行，比如这么写：

c;
f(a,b){
    c=a+b;
}
main(a,b){
    scanf("%d%d",&a,&b);
    printf("%d",f(a,b));
}

汇编代码是：

push    rbp
mov     rbp, rsp
mov     DWORD PTR [rbp-4], edi
mov     DWORD PTR [rbp-8], esi
mov     edx, DWORD PTR [rbp-4]
mov     eax, DWORD PTR [rbp-8]
add     eax, edx
mov     DWORD PTR c[rip], eax
nop
pop     rbp
ret

注意这里必须要用全局变量，使得编译器使用 eax 并将它保留为正确的值。

最好 gcc -s 看一下汇编代码，确保 eax 是对的，这里最后一行 mov 是把 eax 粘贴到全局变量。

内嵌汇编

原理是某些参数是函数的东西，例如 qsort 等，传入的函数实际上是一个函数指针，指向函数的开头。相比于定义函数，有时候自己写汇编代码会更短一些，可以将汇编代码转成 ascii 字符，然后作为字符串参数传入进去。

由于这个操作比较高端，而且大概率用不到，这里不展开，感兴趣自行了解。

常见语法

读取数据

有时候可以循环融合，所以不会去宏定义 for，这样可以更短，i 需要做全局变量让初值为 0。

for(i=0;i<N;++i)scanf("%d",&v[i]);
for(;i<N;)scanf("%d",v+i++);

融合嵌套循环

for(i=0;i<m;puts(v[i++]))for(j=0;j<n;)printf("%d\n",j++);
for(j=i=0;i<m;)j<n?printf("%d\n",j++):(puts(v[i++]),j=0);

main 递归

c;gcd(a,b){c=b?gcd(b,a%b):a}main(a,b){scanf("%d%d",&a,&b);printf("%d",gcd(a,b));}
main(a,b){scanf("%d",&b);b?main(b,a%b):printf("%d\n",a);}

算法改进

以上技巧玩的再溜都比不过算法小手抖一抖。

题面

在数轴上的两点之间，按照下面的规则移动：

每一步的步幅都要是自然数.
同时必须与前一步的步幅相同或者是差 1.
第一步和最后一步的步幅必须是 1.

一共 $n$ 个询问，每个询问输入一行两个正整数 $a, b$ 表示起点和终点，保证 $b>a$ 。

算法一

我会化归！

设 $n$ 步最远能走 $f(n)$ 个单位长度，不难证明 $[n, f(n)]$ 个单位长度都可以用 $n$ 步走到。

显然 $f(n)$ 单增，所以对于一个距离 $x$ ，需要找到最小的 $n$ 使得 $f(n)\ge x$ ，此时的 $n$ 便是答案，所以算法分两步：

给一个 $n$ ，计算 $f(n)$ 。
二分或者枚举 $n$ 直到 $f(n)\ge x$ 。

由于逻辑复杂，总之代码不会很短，考虑改进。

算法二

我会递推！

注意到 $f(n)=f(n-1)+\lfloor\frac{n}{2}\rfloor+1$ ，于是可以直接顺序枚举 $n$ ，由 $f(n-1)$ 计算 $f(n)$ ，直到 $f(n)\ge x$ 。

这样逻辑上只有一个过程，代码会短很多。

算法三

我会等差数列求和！

等差数列计算 $f(2k-1)=k^2, f(2k)=k^2+k+1$ ，两个分别带入进去解方程：

k^2\ge x\iff k\ge \sqrt x \iff n=2k-1\ge2\sqrt{x}-1\iff n\ge 2\sqrt{x}-1\\ k^2+k+1\ge x \iff (k+\frac{1}{2})^2\ge x-\frac{3}{4} \iff n=2k \ge 2\sqrt{x-\frac{3}{4}}-1\iff n\ge 2\sqrt{x-\frac{3}{4}}-1

首先分析 $n\ge 2\sqrt x-1$ ，答案可以表示为 $\lceil2\sqrt{x}-1\rceil$ ，但是由于 $-1$ 比较费力，我们可以改成 $\lfloor2\sqrt{x}\rfloor$ ，当然这在 $x$ 是完全平方数时会出问题，这个稍后再说。

接着分析 $n\ge 2\sqrt{x-\frac{3}{4}}-1$ ，同理改写为 $\lfloor2\sqrt{x-\frac{3}{4}}\rfloor$ ，由于 $\sqrt{x-\frac{3}{4}}$ 是个分数，所以这样无论如何都不会出问题。

这样做我们要写一个分支吗？

答案是，当然不用，把之前省掉的条件补充上去，就是 $2k-1=n=\lfloor2\sqrt{x}\rfloor$ 和 $2k=n=\lfloor2\sqrt{x-\frac{3}{4}}\rfloor$ ，然后发现一件事情，只有当 $\lfloor2\sqrt{x-\frac{3}{4}}\rfloor$ 弄出来是偶数，也就是 $2\sqrt{x-\frac{3}{4}}$ 的小数部分不超过 $0.5$ 的时候，才会有这个 $-\frac{3}{4}$ 的操作，我直接大手一挥把这玩意删了，让 $2\sqrt{x-\frac{3}{4}}$ 变成 $2\sqrt{x}$ ，会出问题吗？注意到 $\sqrt{x}$ 是上凸函数，因此做切线过去简单分析一下 $2\sqrt{x}-2\sqrt{x-\frac{3}{4}}$ 的上界，发现不超过 $0.5$ 。

好了所以说答案就是 $\lfloor2\sqrt{x}\rfloor$ 。

回到之前完全平方数的问题，完全平方数的时候答案多了 $1$ ，利用 C++ 的取整特性，减去一个很小的数让它 Round Down 即可。

main(a,b){for(gets(b);~scanf ("%d%d",&a,&b);)printf("%d\n",a=sqrt(b-a)*2-1e-9);}

算法四

我会打表！

算法三太难了，想不到该咋办捏？

感觉上弄出来的公式里面，二次项的系数是 $\frac{1}{2}$ ，所以猜想答案大概率和 $2\sqrt{x}$ 有点关系，所以写个程序输出一下 $x$ ， $2\sqrt{x}$ 和对应的答案看一看：

n	2n	答案
0	0.000000	0
1	2.000000	1
2	2.828427	2
3	3.464102	3
4	4.000000	3
5	4.472136	4
6	4.898979	4
7	5.291503	5
8	5.656854
9	6.000000
10	6.324555	6
11	6.633250
12	6.928203
13	7.211103	7
14	7.483315
15	7.745967
16	8.000000
17	8.246211	8
18	8.485281
19	8.717798

啊，太简单了， $2\sqrt x$ 是整数的时候输出 $2\sqrt{x}-1$ ，其它时候输出 $\lfloor2\sqrt{x}\rfloor$ 就完了， $2\sqrt{x}-1$ 可以用浮点数强转整数的办法减一个 $\epsilon$ 实现。

于是你在没有学过高等数学的前提下做出了这道题。

随堂练习

题面

给定一个正整数 $n$ ，问 $n$ 有多少种办法写成连续自然数的和。

例如 $15$ ，可以写成：

1+2+3+4+5=15
4+5+6=15
7+8=15
15=15

答案是 $4$ 。

挑战

我的代码长度为 65 字符，尝试将你的代码控制在 100 字符以内。